
9月26日上午,应数学与统计学院邀请,美国Yeshiva大学陈文雄教授通过腾讯会议平台在线做了一场题为《A priori estimate for solutions of nonlocal equations》的学术报告。报告会由数学与统计学院院长蔡礼明教授主持,学院部分老师和研究生聆听了此次报告。
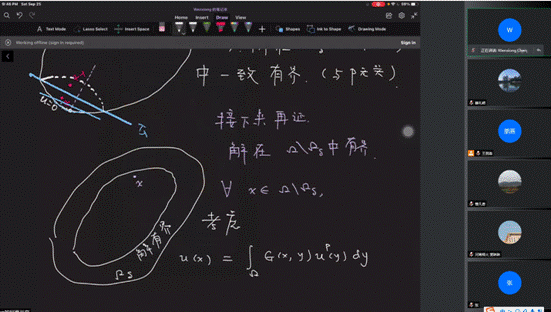
在报告中,陈教授首先介绍了分数阶算子及高阶分数阶算子的定义。接着,陈教授讲解了具有临界指标的高阶分数阶方程正解的一致先验估计定理及证明的主要思想,并首次引入了结合局部移动平面法和格林函数的新方法。与整数阶和分数阶方程先验估计的结果相比,通过新方法获得的高阶分数阶方程正解的一致先验估计与方程非线性项的指数无关。最后,陈教授也指出,该先验估计结合拓扑度理论和连续性方法可用于解的存在性的证明。为了让大家对问题有更好的理解,陈文雄教授在报告中用板书详细地为大家进行讲解
报告结束后,陈文雄教授针对师生们提出的问题给出了详细的解答,并给出了一些与高阶分数阶方程有关的可进一步研究的问题。此次学术报告会让我院师生对高阶分数阶方程的研究有了更加深入的理解。
陈文雄,Yeshiva大学终身教授,数学系主任,博士生导师,南开大学特聘讲座教授,多次获得美国国家科学基金奖。陈文雄教授是偏微分方程和几何分析的杰出专家,研究领域包括非线性偏微分方程、几何分析、非线性泛函分析等。陈教授担任Nonlinear Analysis: Theory, Methods &Applications和Communications onPure and Applied Analysis两个SCI数学杂志的编委,被多个SCI期刊评为优秀审稿人,在数学顶级期刊Annals of Math, J. of Diff. Geom., Comm. Pureand Appl. Math, Duke Math. J, Advance in Math, Arch. Rat. Mech. Anal.等发表论文80余篇,并出版了三本专著,他引已达五千余次,其中在Duke Math. J.上发表的名为Classification of solutions of some nonlinear ellipticequations的论文被引次数高达900余次。